Welcome to the first post of our series on understanding Convolution Neural Networks. In this series we’ll explore the inner workings of CNNs, starting from the basics and gradually delving into advanced concepts.
Today, we’ll begin by discussing the fundamental concept of convolution.
Convolution Neural Network (CNN or ConvNet) is a computer algorithm designed to recognize patterns in images.
It’s inspired by how the brain’s visual cortex works. Just like how we identify objects by recognizing their features (like shapes and colors), a CNN learns to do the same by analyzing different parts of images and learning what patterns represent different objects and features.
Let’s begin!
Overview
Table of Contents
What Do We Mean by Convolution?
Convolution is a mathematical operation that combines two signals and is denoted by asterisks (*).
Here’s an example where we have a time series “a” and we want to convolve it on an array “b” of 3 elements:
import numpy as np
# Define the array 'a' and the filter 'b'
a = np.array([1, 2, 3, 6, 7, 4, 9, 10])
b = np.array([1/3, 1/3, 1/3])
# Perform convolution
result = np.convolve(a, b, mode='valid')
print("Result of convolution:", result)Here, each element of the filter “b” is multiplied by the corresponding element in the array “a”, and then these products are summed up to produce a single output value. This process is repeated by shifting the filter over the array in a sliding window manner.
Technically, what we just did is cross-correlation. For this to be convolution, we’ll have to flip the filter “b”.
However, in neural networks, the terms cross-correlation and convolution are used interchangeably.
You might think, why would we want to flip one of the inputs?
Doing so makes convolution operation commutative (order of operands does not matter), meaning:
a*b = b*aHowever, in cross-correlation, we have:
a*b \neq b*aCommutative property is not very crucial in neural networks. Since the weights (kernels) are learned during training the network adjusts itself accordingly. So there’s no need to flip one of the inputs.
ii. Convolving Edge Detection Filter on Time Series Array
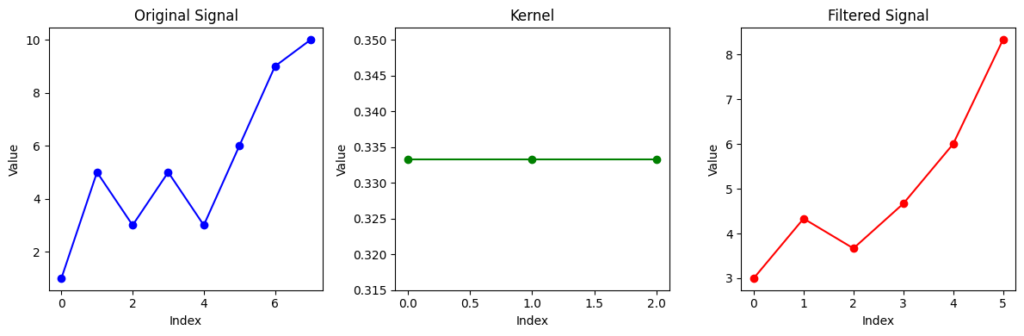
In the example we saw earlier, the filter ‘b’ computes the local averages by averaging the values in the windows. Let’s see how it looks if we plot it:
import numpy as np
import matplotlib.pyplot as plt
# Define the original signal
signal = np.array([1, 5, 3, 5, 3, 6, 9, 10])
# Define the filter
filter_b = np.array([1/3, 1/3, 1/3])
# Perform the convolution
filtered_signal = np.convolve(signal, filter_b, mode='valid')
# Plot the kernel, original signal, and filtered signal in one row
plt.figure(figsize=(12, 4))
# Plot the original signal
plt.subplot(1, 3, 1)
plt.plot(signal, marker='o', color='b')
plt.title('Original Signal')
plt.xlabel('Index')
plt.ylabel('Value')
# Plot the kernel
plt.subplot(1, 3, 2)
plt.plot(filter_b, marker='o', color='g')
plt.title('Kernel')
plt.xlabel('Index')
plt.ylabel('Value')
# Plot the filtered signal
plt.subplot(1, 3, 3)
plt.plot(filtered_signal, marker='o', color='r')
plt.title('Filtered Signal')
plt.xlabel('Index')
plt.ylabel('Value')
plt.tight_layout()
plt.show()As you can see, the filtered signal is the smoothed version of the original signal.
ii. Convolving Edge Detection Filter on Input Image
We can also extend this concept to 2-Dimensions. Here is an example that detects vertical edges from a 8×8 image. Here we are generating an input image with first four columns with value 0 (indicating black) and remaining 4 columns with value 1 (indicating white):
import numpy as np
from scipy.signal import convolve2d
# Create the input image
input_image = np.zeros((8, 8))
input_image[:, 4:] = 1
# Define the filter
filter = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
# Perform the convolution
convolved_image = convolve2d(input_image, filter, mode='valid')
# Print the matrix output
print("Input Image:")
print(input_image)
print("\nVertical Edge Detection Filter:")
print(filter)
print("\nConvolved Image:")
print(convolved_image)Here’s what the values of the matrices look like:

One last thing before moving on, you might have noticed that our resultant image is of size 6×6, why isn’t it the same as the input image?
When we apply a filter to an image using convolution, the size of the output image may differ from the input image, depending upon factors such as the size of the filter and the padding applied.
In this case, the input image is 8×8 and the filter is 3×3, for simplicity, no padding is applied. Since the padding is missing, the filter cannot be applied to the edges of the input image, thus reducing the size of the resultant image.
Here’s the formula to calculate the output size:
Output Size = (\frac{input size - filter + 2 * padding}{stride})+1 Output Size = (\frac{8- 3 + (2 * 0)}{1})+1 = 5+1 = 6That’s why the resultant image is 6×6. If you want the output size to be the same as the input, use padding!
iii. Convolving Edge Filter on GrayScale Image
Let’s now see an example of a grayscale image and detect edges in the vertical direction only:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# Load your grayscale image
image = cv2.imread('/content/flower.png', cv2.IMREAD_GRAYSCALE)
# Define the vertical edge detection filter
vertical_edge_filter = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
# Perform the convolution
convolved_image = cv2.filter2D(image, -1, vertical_edge_filter)
# Display the original and convolved images
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('Original Image')
plt.axis('off')
plt.subplot(1, 2, 2)
plt.imshow(convolved_image, cmap='gray')
plt.title('Vertical Edge Detection')
plt.axis('off')
plt.tight_layout()
plt.show()
We applied a handcrafted vertical edge detection filter and it gave us a feature map that highlights vertical edges. Here is what it looks like:

Here is what it would look like if we detect horizontal edges:

We can also try this on colored images.
Is the concept of convolution limited to only images and signals? or can we use it on other types of data?
Apply Convolutions on Data Beyond Signals and Images
Convolutions can be applied to various types of data, here are some of them:
i. Audio Signals
In audio processing, you can use convolutions for various tasks including filtering and echo cancellation.
For instance, you can convolve an audio signal with an impulse response to simulate the effect of a room’s acoustics.
ii. Videos
Videos are essentially sequences of images (frames) captured over time. Convolution is frequently used in video processing for tasks such as noise reduction motion detection, and object tracking.
For instance, you can convolve a video frame with a spatiotemporal filter to detect moving objects to enhance features in the video.
iii. Electrocardiograms (ECGs)
ECGs represent the electrical activity of the heart over time. You can apply convolution to analyze ECG signals for tasks such as noise removal, feature extraction, and heartbeat detection.
To Know More About Convolutions
- Convolutional Neural Networks – Coursera
- Understanding Convolution Operations In Neural Networks – Deep Lizard



